Вывод передаточной функции
Dz (обсуждение | вклад) |
Dz (обсуждение | вклад) |
||
| Строка 20: | Строка 20: | ||
Отсюда получаем: | Отсюда получаем: | ||
<math> \frac{\partial (\phi)}{\partial F_{II}} \Delta F_{II} + \frac{\partial (\phi)}{\partial L_{II}} \Delta L_{II} = \frac{d (\Delta L_{II} \rho)}{d t}</math> | <math> \frac{\partial (\phi)}{\partial F_{II}} \Delta F_{II} + \frac{\partial (\phi)}{\partial L_{II}} \Delta L_{II} = \frac{d (\Delta L_{II} \rho)}{d t}</math> | ||
| + | |||
Подставим значения производных: | Подставим значения производных: | ||
<math> - \rho \Delta F_{II} = \frac{d (\Delta L_{II} \rho)}{d t}</math> | <math> - \rho \Delta F_{II} = \frac{d (\Delta L_{II} \rho)}{d t}</math> | ||
| + | |||
| + | |||
| + | <math> - \Delta F_{II} (t) = \frac{d (\Delta L_{II} (t) )}{d t}</math> | ||
| + | |||
| + | |||
| + | Преобразуем по Лапласу: | ||
| + | |||
| + | <math> - \Delta F_{II} (p) = p \Delta L_{II} (p)</math> | ||
Версия 00:54, 25 мая 2016
Рассмотрим пример вывода передаточной функции выпарного аппарата по каналу 
(расход упаренного раствора из выпарного аппарата II - уровень в выпарном аппарате II).
В аппарат входит поток упариваемого раствора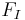 
, выходит поток упареного раствора с расходом 
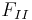и поток пара к конденсатору 
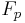. Также поступает поток тепла от рубашки, в которой конденсируется пар, отходящий от выпарного аппарата I. Теплопотерями пренебрегаем, свойства раствора (плотность, теплоёмкость и т.д.) считаем постоянными, изменением коэффициента теплопередачи пренебрегаем.
В данном случае передаточную функцию можно вывести из материального баланса по раствору в целом:
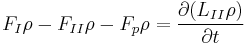
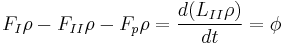
В стационарном режиме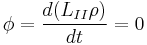 
Малое отклонение от стационарного режима:
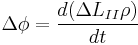
Разложим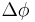 
в ряд Тейлора с удержанием членов первого порядка малости:
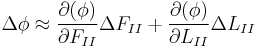
Отсюда получаем:
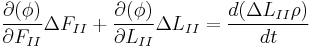
Подставим значения производных:
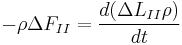
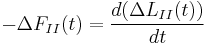
Преобразуем по Лапласу:
