Wiki Легостаев

Версия 08:32, 22 декабря 2025

Файл:Вик1.jpg

'Полужирное начертание'Алгоритм Дейкстры — алгоритм на графах, изобретённый нидерландским учёным Эдсгером Дейкстрой в 1959 году. Находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса.

Математическое описание

Алгоритм Дейкстры использует жадную стратегию. Для каждой вершины v хранится текущая длина кратчайшего пути из начальной вершины s в v, а также булевый флаг — посещена ли вершина.

Изначально , для всех остальных вершин расстояние считается бесконечным (), .

На каждом шаге алгоритма выбирается вершина 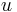с минимальным среди ещё не посещённых. Для каждого соседа 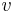вершины 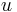пересчитывается расстояние:

где 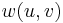— вес ребра из 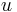в .

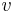Алгоритм завершается, когда все вершины посещены или минимальное расстояние среди непосещённых равно бесконечности.

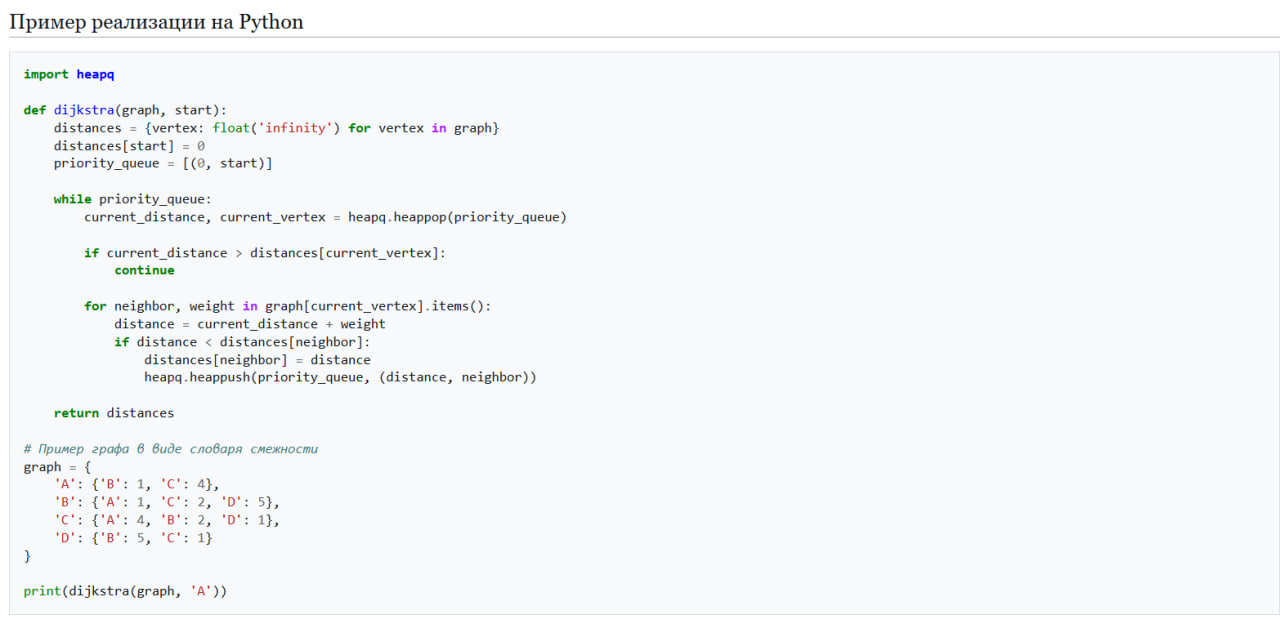
Пример реализации на Python

<syntaxhighlight lang="python"> import heapq

def dijkstra(graph, start):

   distances = {vertex: float('infinity') for vertex in graph}
   distances[start] = 0
   priority_queue = [(0, start)]

   while priority_queue:
       current_distance, current_vertex = heapq.heappop(priority_queue)

       if current_distance > distances[current_vertex]:
           continue

       for neighbor, weight in graph[current_vertex].items():
           distance = current_distance + weight
           if distance < distances[neighbor]:
               distances[neighbor] = distance
               heapq.heappush(priority_queue, (distance, neighbor))

   return distances

1. Пример графа в виде словаря смежности

graph = {

   'A': {'B': 1, 'C': 4},
   'B': {'A': 1, 'C': 2, 'D': 5},
   'C': {'A': 4, 'B': 2, 'D': 1},
   'D': {'B': 5, 'C': 1}

}

print(dijkstra(graph, 'A')) </syntaxhighlight>

Химическая аналогия

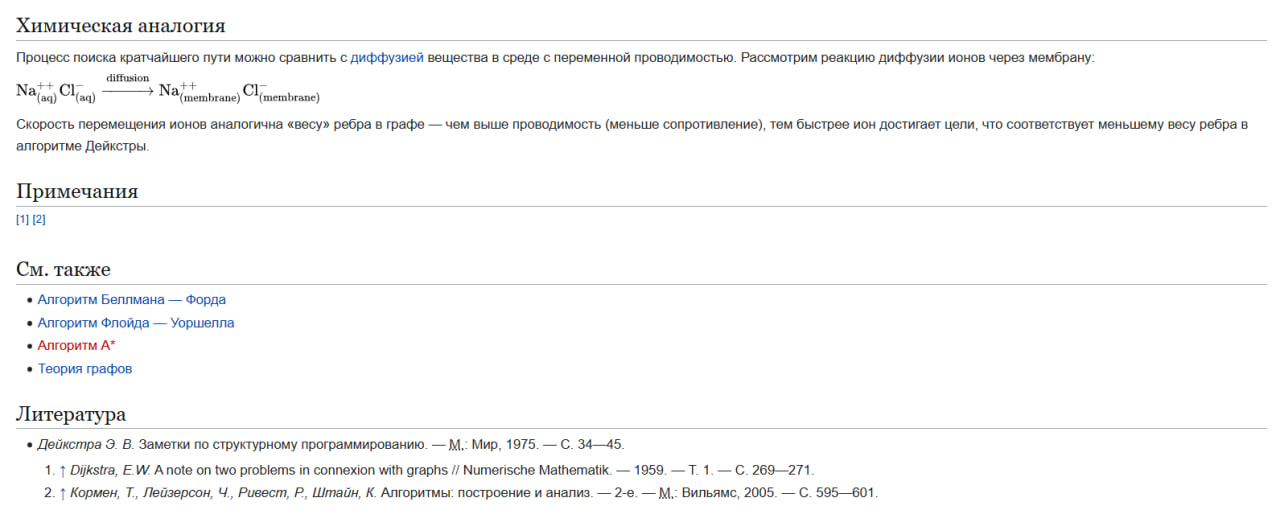
Процесс поиска кратчайшего пути можно сравнить с диффузией вещества в среде с переменной проводимостью. Рассмотрим реакцию диффузии ионов через мембрану:

<chem>Na^+_{(aq)} + Cl^{-}_{(aq)} ->[\text{diffusion}] Na^+_{(membrane)} + Cl^{-}_{(membrane)}</chem>

Скорость перемещения ионов аналогична «весу» ребра в графе — чем выше проводимость (меньше сопротивление), тем быстрее ион достигает цели, что соответствует меньшему весу ребра в алгоритме Дейкстры.

Примечания

Шаблон:Примечания <ref name="Dijkstra1959">Шаблон:Статья</ref> <ref name="Cormen">Шаблон:Книга</ref>

См. также

• Алгоритм Беллмана — Форда
• Алгоритм Флойда — Уоршелла
• Алгоритм A*
• Теория графов

Литература

• Шаблон:Книга