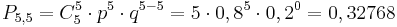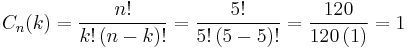Пример для Ивана
Материал из Wiki
(Различия между версиями)
Dz (обсуждение | вклад) |
Dz (обсуждение | вклад) |
||
| Строка 6: | Строка 6: | ||
Событие <math>{\displaystyle A}</math> - выбрали учителя женщину. вероятность <math>{\displaystyle p}=0,8</math> <math>{\displaystyle q}=1{\displaystyle p}=1-0,8=0,2</math> | Событие <math>{\displaystyle A}</math> - выбрали учителя женщину. вероятность <math>{\displaystyle p}=0,8</math> <math>{\displaystyle q}=1{\displaystyle p}=1-0,8=0,2</math> | ||
| + | |||
| + | |||
| + | |||
Вероятность того, что 4 женщины, 1 мужчина: | Вероятность того, что 4 женщины, 1 мужчина: | ||
<math> | <math> | ||
| Строка 13: | Строка 16: | ||
<math> | <math> | ||
{\displaystyle C_{n}(k)={\frac {n!}{k!\left(n-k\right)!}}}= {\frac {5!}{4!\left(5-4\right)!}}= {\frac {120}{24\left(1\right)}}=5 | {\displaystyle C_{n}(k)={\frac {n!}{k!\left(n-k\right)!}}}= {\frac {5!}{4!\left(5-4\right)!}}= {\frac {120}{24\left(1\right)}}=5 | ||
| + | </math> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Вероятность того, что 5 женщин, 0 мужчин: | ||
| + | <math> | ||
| + | P_{5,5}=C_5^5\cdot p^5 \cdot q^{5-5}=5 \cdot 0,8^5 \cdot 0,2^0=0,32768 | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | {\displaystyle C_{n}(k)={\frac {n!}{k!\left(n-k\right)!}}}= {\frac {5!}{5!\left(5-5\right)!}}= {\frac {120}{120\left(1\right)}}=1 | ||
</math> | </math> | ||
Версия 23:47, 26 сентября 2016
Если вероятность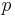 
наступления события 
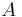в каждом испытании постоянна, то вероятность 
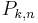того, что событие 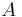наступит ровно 
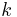раз в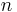 
независимых испытаниях, равна
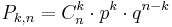
Событие 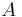- выбрали учителя женщину. вероятность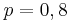 
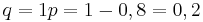
Вероятность того, что 4 женщины, 1 мужчина:
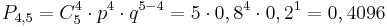
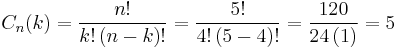
Вероятность того, что 5 женщин, 0 мужчин:
